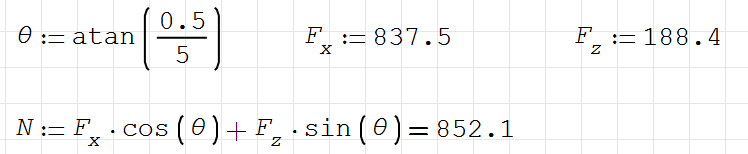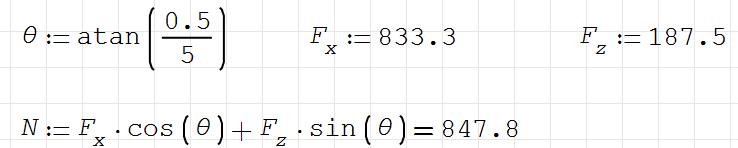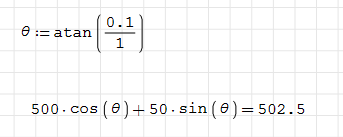[Improvement] Eccentricity in Cross Section Affects the Internal Forces?

[netsonic_Sofistik]

Generally, the beam nodal line (NL) and line of gravity center (CGL) of each section will be the same, if eccentricity is not used for cross section.
If the eccentricity is uded for cross section, the NL and CGL will be different.

E.g.
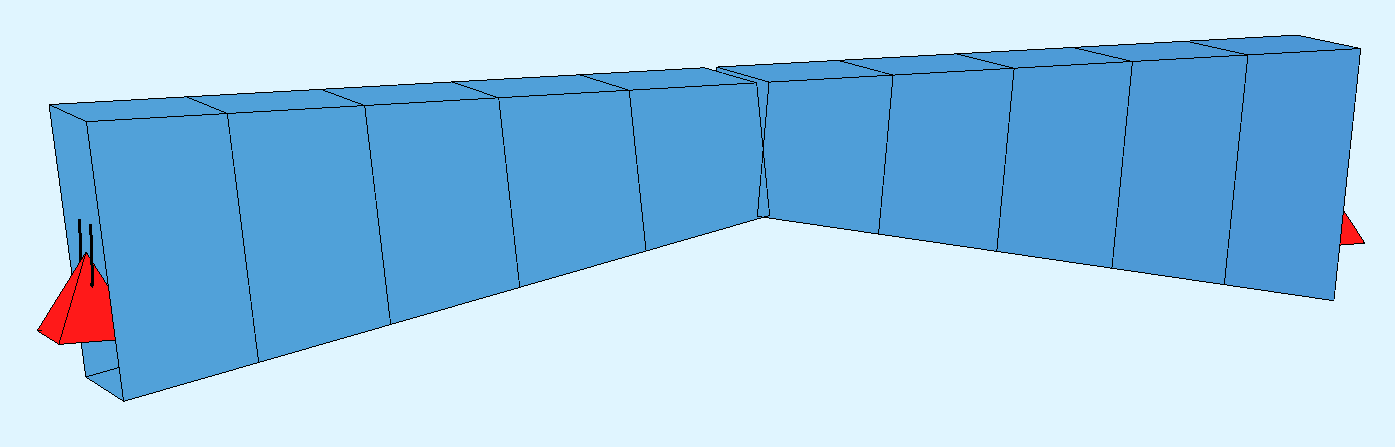
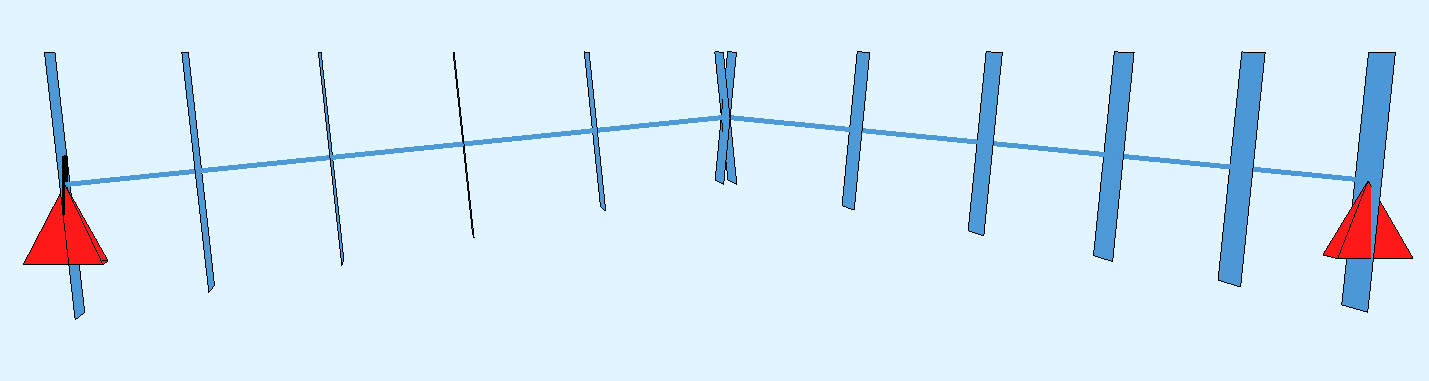
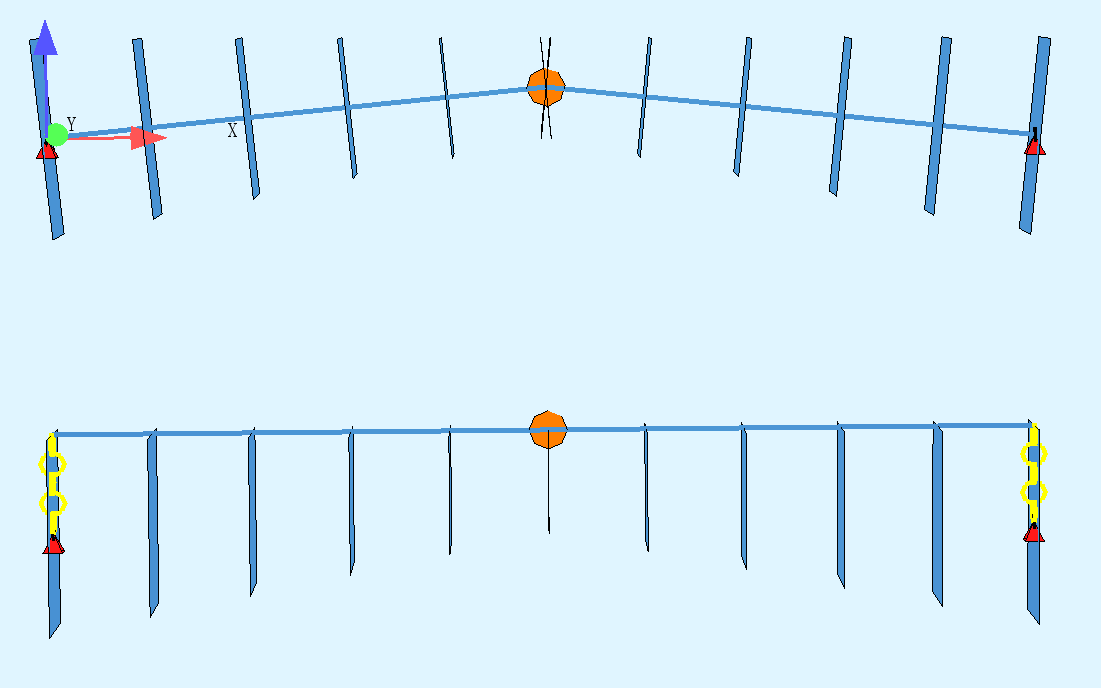
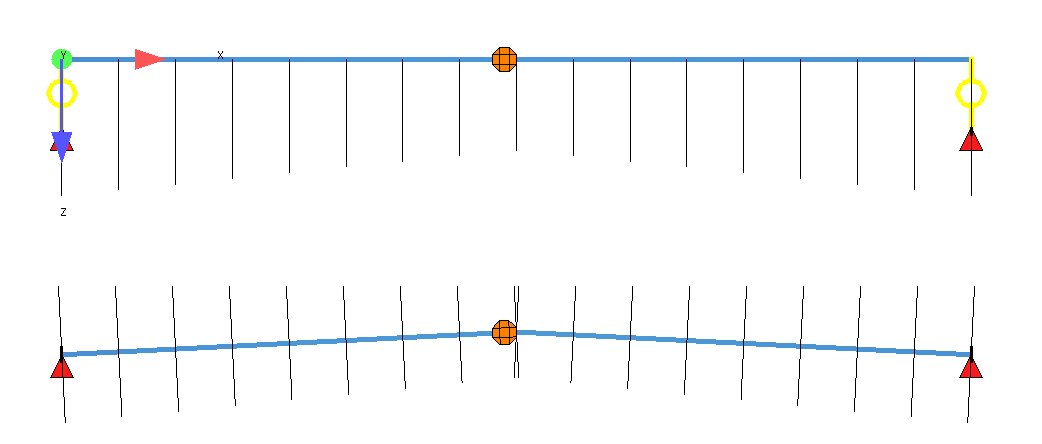
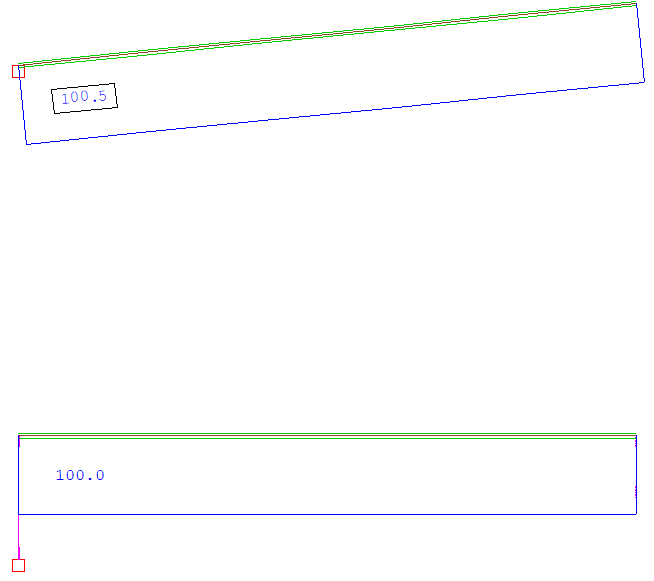
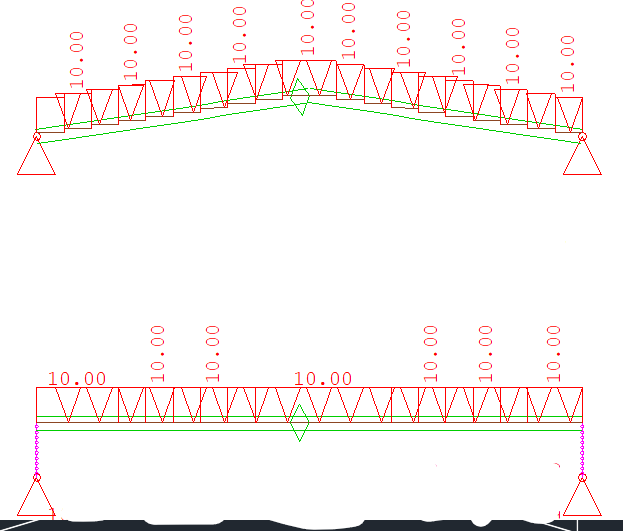
I have an 10m arch-like structure, the end section is 1m (B) x 2m (H) rectangle, while the mid section is 1m (B) x 1m (H) rectangle. The top of the beam is aligned.
I use two different approach to model the structure:

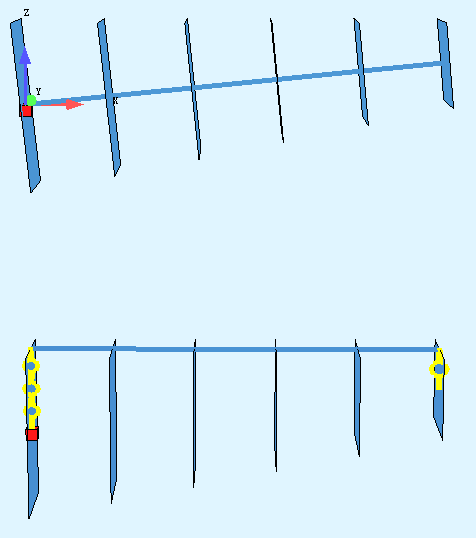
1. The nodes are the same as gravity center of each section, I call it CGL Arch.
2. The nodes are on the top-center of beam, I call it NL Arch. (It looks like a beam, but it behaves like an arch)

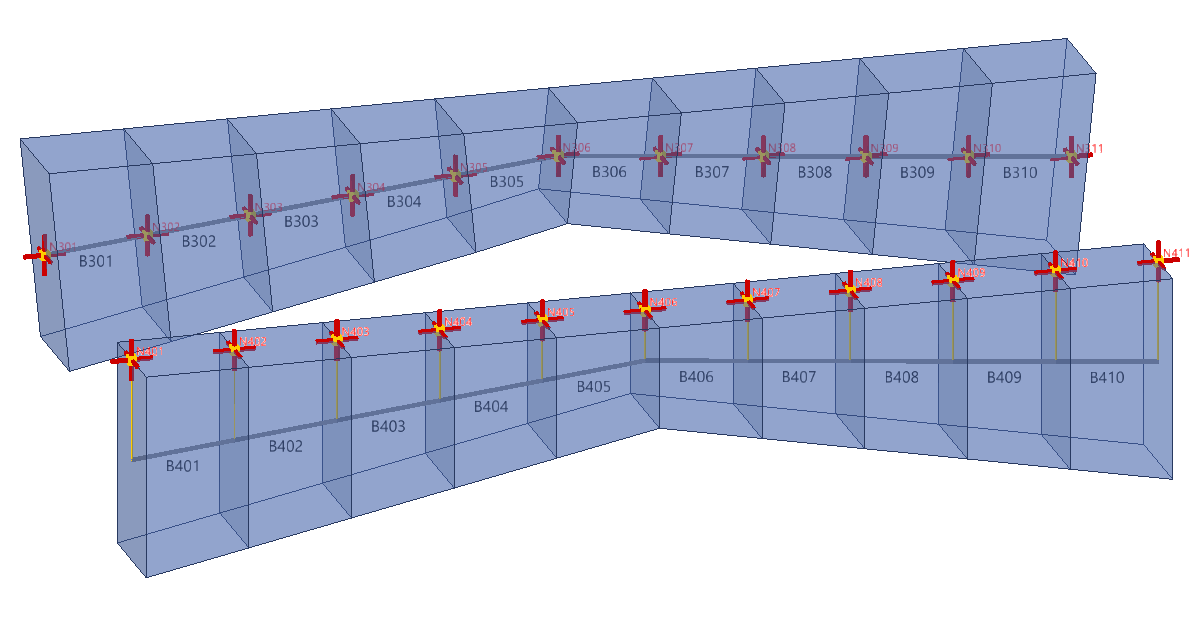
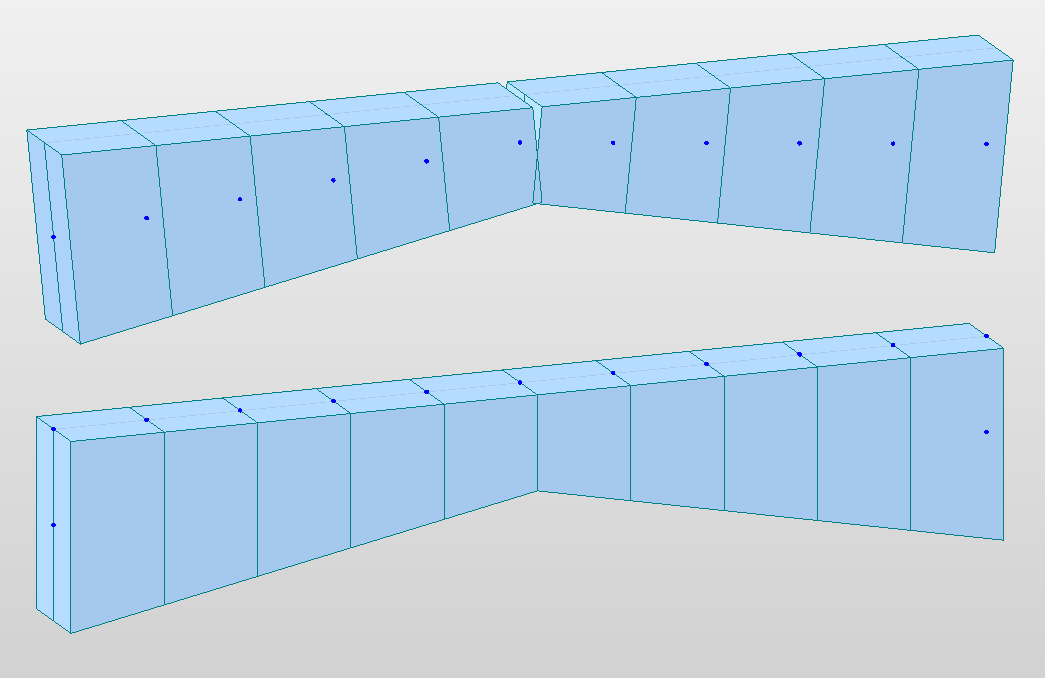
CGL Arch

NL Arch

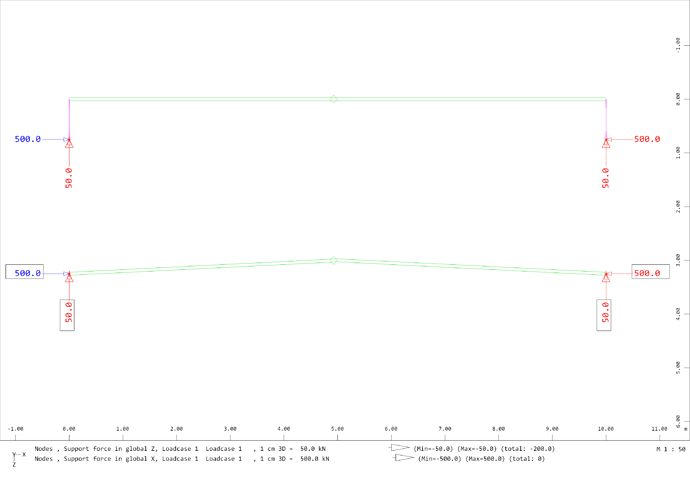
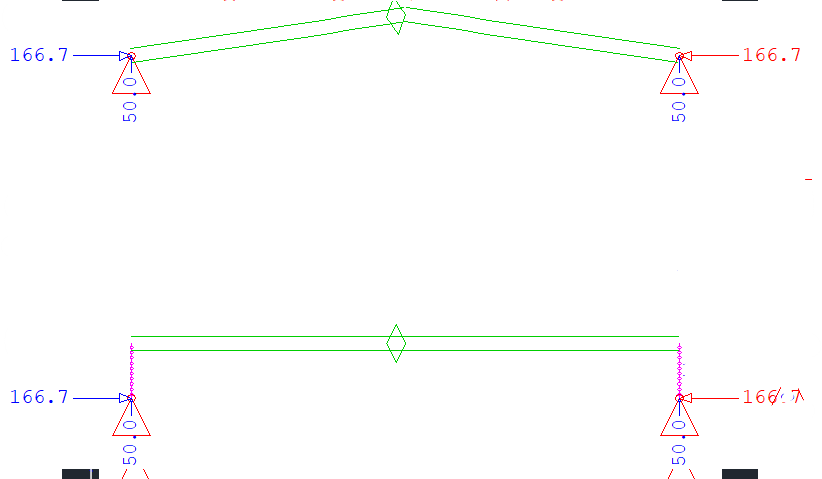
The supports are the same for both arches, they are on the gravity center of end sections.
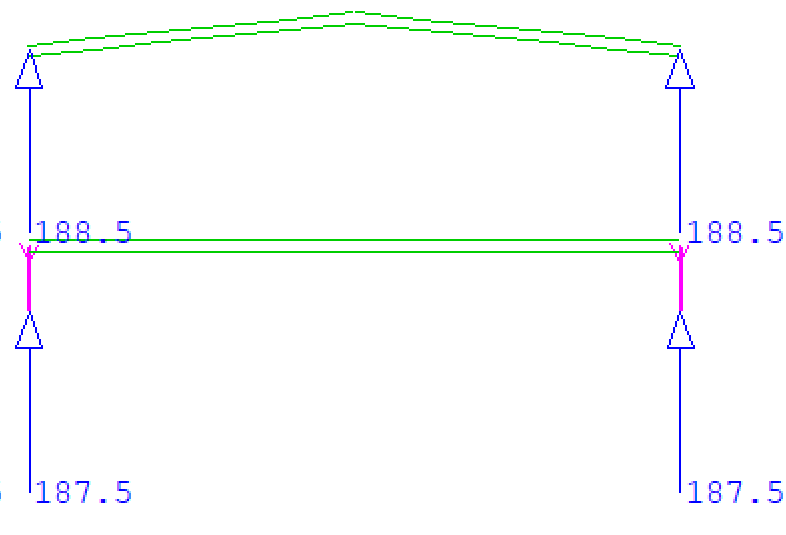
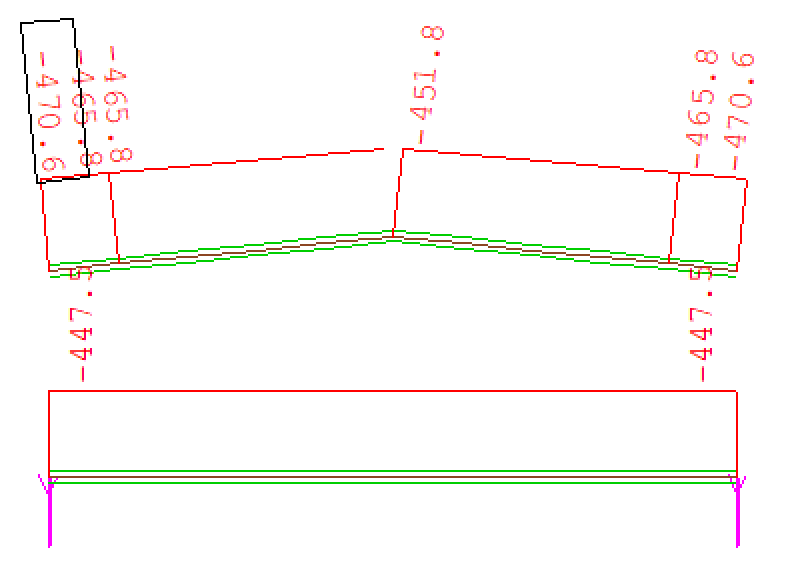
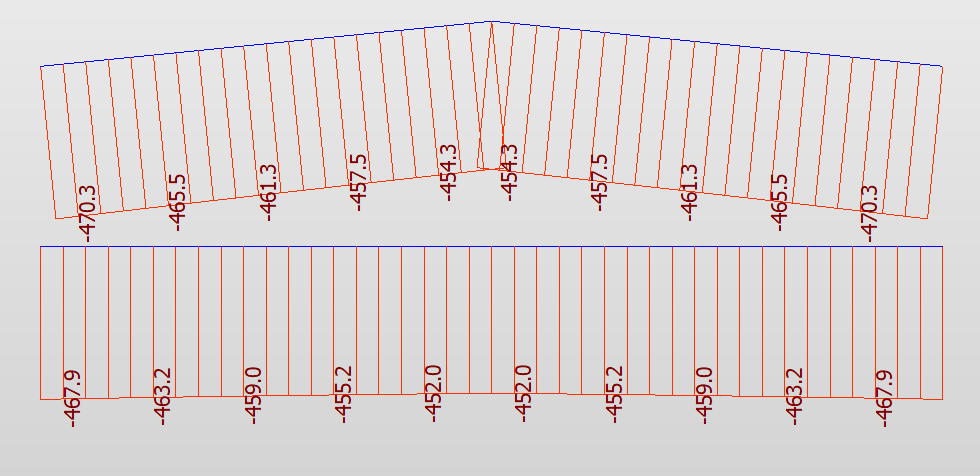
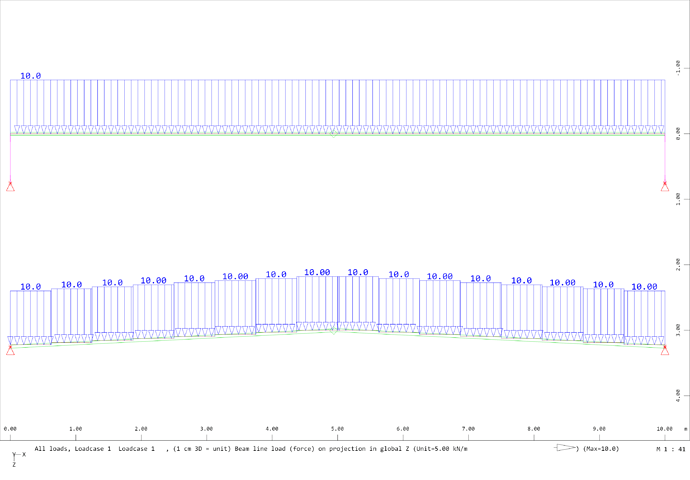
These are the reactions for both arches under self weight.

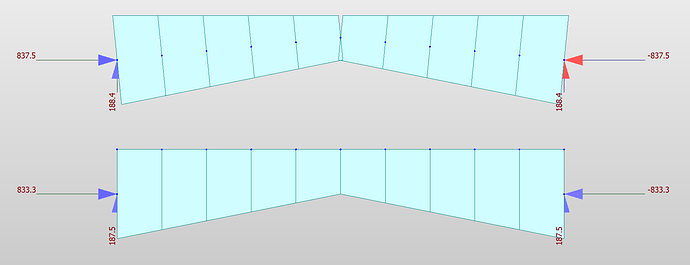
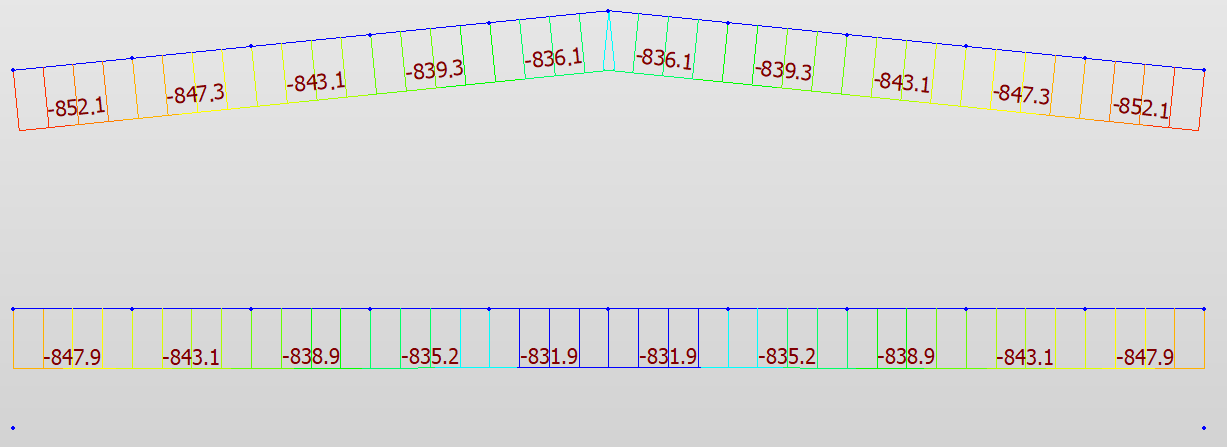
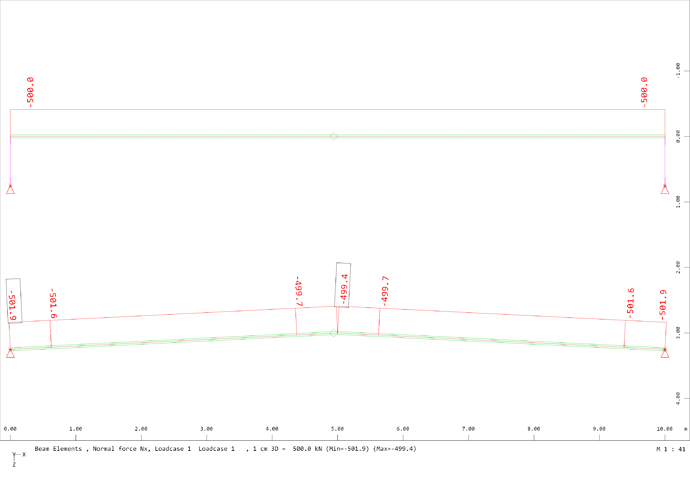
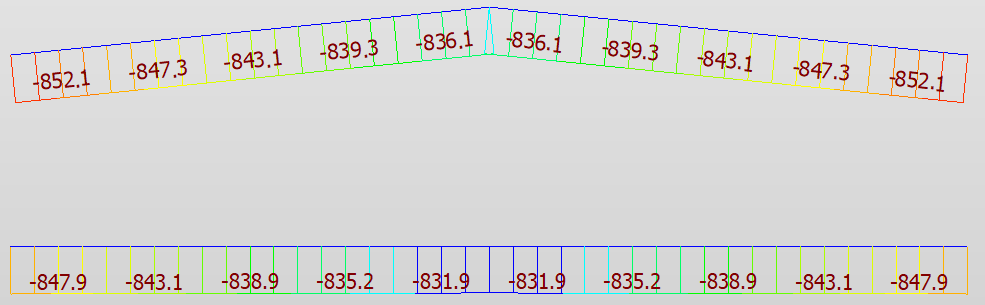
These are the axial forces for both arches under self weight.

You can see that the axial forces are DIFFERENT.
The slope of CGL of the arch is 0.5/5=0.1, angle=atan(0.1)=5.71deg
For CGL Arch, N=188.5sin(5.71)+454.1cos(5.71)=471kN = 470.6kN from Sofstik
For NL Arch, N=187.5sin(0)+447.5cos(0)=447.5kN = 447.5kN from Sofstik

Obvioulsy, Sofistik use NL, not the CGL to interpret internal forces, which is MISLEADING.

Other softwares, like RM Bridge (TDV), Midas Civil, use CGL to interpret internal forces.
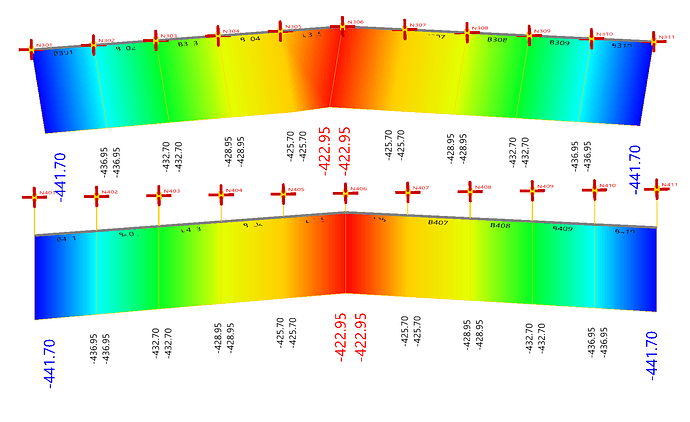
RM Bridge:

The top dirgram is the axial force in CGL Arch, the bottom dirgram is the axial force in NL Arch, they are the same.

Midas Civil:

The top dirgram is the axial force in CGL Arch, the bottom dirgram is the axial force in NL Arch, they are almost the same.

[sfr]

Since your reaction forces differ my guess is you have applied a line force and related it to the length of the beam (i.e. system line).

The results you get ARE the internal forces related to the center of gravity.
However you are applying different loadings on the two systems and the loading can be controlled using the correct reference system and projection. (Beam: Type, Ref, Reft in sofiload)

I also suggest you use a statically determinate structure (like a cantilever beam) if you are going to study load application/internal forces. Often the difference between systems is due to the modelling errors not easily discovered in indeterminate systems.

[netsonic_Sofistik]

@ sfr
The difference of reactions between CGL model and NL model is due to the different lengthes of each beam element. For CGL mode, each element is (1^2+0.1^2)^0.5=1.005m, while each element is 1m in NL model. I apply the same load (self-weight) to all the models.

I made a statically determinate structure by release the moment at mid-span.

The top one is the CGL model, the bottom is the NL model.

Here is my Hand calculation:
The γ=25kN/m3,
the end section is 2m by 1m, p1=25x2x1=50kN/m
the mid section is 1m by 1m, p2=25x1x1=25kN/m
The span is 10m, the rise of arch is 0.5m, the support is at center of gravity.

So the vertical reaction is Rz=0.5x(50+25)x10/2=187.5kN
the horizontal reaction is Rx=(0.5x50x5x1/3x5+0.5x25x5x2/3x5)/0.5=833.3kN
The slope angle is θ=atan(0.5/5)

The axial force at support should be 833.3cos(θ)+187.5sin(θ)=847.8kN
The Midas Civil shows 847.9kN for NL model, which concludes that Midas Civil use CGL to get axial force;
while Sofistik shows 833.4kN for NL model, which concludes that it use NL to get axial force.

Below are the reactions from Midas Civil, top is the CGL model, bottom is the NL model

Below are the axial force, top is the CGL model, bottom is the NL model

Hand calculaton to verify that Midas Civil use CGL to get Axial force for both CGL and NL models
CGL Model:

NL model (the axial force is along the CGL not along the NL)

Below are the reactions from Sofistik, top is the CGL model, bottom is the NL model

Below are the axial force, top is the CGL model, bottom is the NL model

As for CGL Model, the NL line is the same as CGL line, the axial force along NL line (CGL line) is

which is same as that from Sofistik.
As for NL model, the axial force equals to the horizontal reaction 833.4kN.

You can find that

1. the reactions from Midas Civil and Sofistik are the same
2. the axial force in CGL models from Midas Civil and Sofistik are the same
3. the axial force in NL models from Midas Civil and Sofistik are different

Therefore we can conclude that Sofistik use NL, not CGL to interpret the internal force,
which is Misleading.

[TomazSabec]

Tried the same thing. I get minimum difference.

[netsonic_Sofistik]

@ TomazSabec
I assume the slope of you arch = 0.1/1=10%

So the axial force in the CGL model (your bottom model) is

which is close to 501.9 from your Sofistik result, this axial force is along the CGL and NL.
In CGL case, the NL is the same as CGL.

While the axial force in the NL model (your top model) is 500kN, which equals to your horizontal reaction, which concludes that the axial force is along the NL. not the CGL.

[sfr]

I’m sorry but you have:

• 2 different models
• 3 different fe-programs
• 5 different reaction forces (same total reaction force in RM bridge only)

You clearly are applying different LOADINGS to the various models.
The internal forces in sofistik are related to the center of gravity (or shear center), read the AQB manual chapter 2.3.

If you want to compare internal forces of two models, you should make sure you actually apply the same loading (which you are not).

The difference between your models are due to different loadings and perhaps also a difference in the structural model itself.
Not that the internal forces are related to the system line.

I suggest you model an eccentric and a centric cantilever beam and apply compressive point loads to the end. Then you will see that the normal force is with respect to the center of gravity.

[netsonic_Sofistik]

@ sfr

2 different models:
one is CGL model, the node is at center of gravity

the other one is NL model, the node is at top center.

“If you want to compare internal forces of two models, you should make sure you actually apply the same loading (which you are not).”
I apply the self-weight in Sofistik for both CGL and NL models

PROG	Sofiload	urs:3
HEAD
LC	1	FACD	1	TITL	‘Self-weight’

1. Hand Calculation for NL model, CGL model is similar.

The γ=25kN/m3,
the end section is 2m by 1m, p1=25x2x1=50kN/m
the mid section is 1m by 1m, p2=25x1x1=25kN/m
The span is 10m, the rise of arch is 0.5m, the support is at center of gravity.
So the vertical reaction is Rz=0.5x(50+25)x10/2=187.5kN
the horizontal reaction is Rx=(0.5x50x5x1/3x5+0.5x25x5x2/3x5)/0.5=833.3kN
The slope angle is θ=atan(0.5/5)
The axial force at support should be 833.3cos(θ)+187.5sin(θ)=847.8kN

2. Midas Results
Below are the reactions from Midas Civil, top is the CGL model, bottom is the NL model

The tiny difference of reactions between CGL model and NL model is due to the element length.
For CGL mode, each element is (1^2+0.1^2)^0.5=1.005m
For NL mode, each element is 1.0m
Below are the axial force, top is the CGL model, bottom is the NL model

Hand calculaton to verify that Midas Civil use CGL to get Axial force for both CGL and NL models
CGL Model:

NL model (the axial force is along the CGL not along the NL)

3. Sofistik Results
Below are the reactions from Sofistik, top is the CGL model, bottom is the NL model

Below are the axial force, top is the CGL model, bottom is the NL model

As for CGL Model, the NL line is the same as CGL line, the axial force along NL line (CGL line) is

which is same as that from Sofistik.
As for NL model, the axial force equals to the horizontal reaction 833.4kN.

4. Comparison and Conclusion
As for CGL Model, Midas Civil and Sofistik have the same axial force 852.1kN
As for NL Model. hand caulation and Midas Civil have the very close axial force 847.8(9)kN,
while Sofistik has axial force 833.4kN, which equal to horizontal reaction, and which is along the NL, not CGL.

This concludes that for NL model, Sofistik use NL not CGL to interpret internal force.

[sfr]

Total vertical reaction force:

• CGL R=2*188.4=376.8 kN
• NL R=2*187.5=375.0 kN

→ The loads aren’t the same
→ The stiffnesses of the systems might not be the exact same (however you can’t see that until you correct the loads, perhaps a UDL load?)
→ You can’t draw conclusions regarding internal forces due to the errors/differences above

[netsonic_Sofistik]

→ The loads aren’t the same
The difference are due tiny element lenght difference: 1.005m for CGL and 1.0m for NL

• CGL R=2x(50+25)/2x10x1.005/2=2x188.4=376.8 kN
• NL R=2x(50+25)/2x10x1.0/2=2x187.5=375.0 kN

→ The stiffnesses of the systems might not be the exact same (however you can’t see that until you correct the loads, perhaps a UDL load?)
It’s a statically determinate structure (as you request) , which means internal force has nothing to do with the stiffness

→ You can’t draw conclusions regarding internal forces due to the errors/differences above
Just compare NL models by hand calculation, Midas Civil and Sofistik， there is no difference or “error” between them.
Hand Calcualtion:
The γ=25kN/m3,
the end section is 2m by 1m, p1=25x2x1=50kN/m
the mid section is 1m by 1m, p2=25x1x1=25kN/m
The span is 10m, the rise of arch is 0.5m, the support is at center of gravity.
So the vertical reaction is Rz=0.5x(50+25)x10/2=187.5kN
the horizontal reaction is Rx=(0.5x50x5x1/3x5+0.5x25x5x2/3x5)/0.5=833.3kN
The slope angle is θ=atan(0.5/5)
The axial force at support should be 833.3cos(θ)+187.5sin(θ)= 847.8kN

Midas Civil

Sofistik

As you can see, and/or as you can infer by Structural Mechanics
the reactions by hand calculation, Midas Civil and Sofistik are the SAME
For the SAME reaction, the structure should get the same axial force at support
Hand calculation and Midas Civil shows 847.8kN for axial force, it’s along CGL
But Sofistik shows 833.4kN, why? because it’s along NL, not CGL, the NL is horizontal, so it equal to horizontal reation 833.4kN.

[netsonic_Sofistik]

@ sfr

I made two simple cantilever beams as you suggested, top one is CGL model, while the bottom one is the NL model.

and I applied point loads at CG of free ends.
The horizontal component of the load is 100kN, since the slope of the CGL is 10%, the vertical component of the load is 10%x100=10kN, therefore the load (100^0.5+10^0.5)=100.5kN is along the CGL.

The axial force of both CGL and NL model should be 100.5kN.

Midas Civil result shows 100.5kN for both CGL and NL model

The Sofistik CGL model shows 100.5kN, but NL model shows 100kN

Does this confirm that Sofistik use NL to interpret internal force?

[sfr]

Well no/yes

• No: The normal force for each element is acting in the center of gravity of the cross section. (This is what I thought you meant originally)
• Yes: The local coordinate system of each cross section is with respect to your system line. (This is probably what you meant all along)

If you perform further analysis on the system with AQB there will be an automatic transformation of the beam forces unless you turn it off.
Ctrl Opt Smoo Val +128/256/512
Hopefully that solves your problem

[netsonic_Sofistik]

Thank you for the “SMOO” tip.
But the AQB manual says “SMOO Smoothing of moments at supports”. While in my case, there is no moment, only axial force at support.

According to ASE manual

2.3.2 Coordinate System of Forces, Center of Gravity
The beam forces N, MY and MZ are related to the center of gravity of the actual active partial
section (not to node connecting line). MT, VY and VZ are related to the center of shear

But the results from ASE doesn’t prove what it says

[sfr]

If you look at the options for ctrl smoo you can also turn off a transformation of forces (e.g. +256).
AQB will transform the system coordinate system to the normal axis of the beam by default (I have used the above option to turn it off, since it was incorrect in my particular case)

Well the ASE manual describes that internal forces have their origin in the center of gravity. If you check your cantilever model you will see that there are no moments in either section (so the statement is correct).
However the section is assumed perpendicular to the system line (just as visualised in the animator, your first picture)

A rotation of the coordinate system to the inclined normal axis should be performed by AQB unless you turn it off with ctrl smoo.

[netsonic_Sofistik]

Thanks you, you always give useful suggestion.

A rotation of the coordinate system to the inclined normal axis should be performed by AQB unless you turn it off with ctrl smoo.

Sofistik should mention this in the ASE manual.

Well the ASE manual describes that internal forces have their origin in the center of gravity. If you check your cantilever model you will see that there are no moments in either section (so the statement is correct).

Thank you for the explanation, but I don’t think so.
I applied the point load at CG, ad its direction is along CGL, so there should be no moment.
But according to ASE manual “The beam forces N is related to the center of gravity of the actual active partial section (not to node connecting line)”, it doesn’t mention any thing about eccentricity of section will affect this or not"

@ JFH
Could you help take a look at this issue?

[netsonic_Sofistik]

If you perform further analysis on the system with AQB there will be an automatic transformation of the beam forces unless you turn it off.
Ctrl Opt Smoo Val +128/256/512

According to AQB manual

The forces and the prestressing tendons can be defined directly or be imported from the
database for beam, truss or cable elements. A whole series of design tasks can be carried
out with the selected forces. These are:
1.Creep and shrinkage analysis (AQBS only)
2.Determination of the maximum stresses in the cross section according to the theory of
elasticity.
3.Determination of the required reinforcement or internal safety factor for unreinforced, re-
inforced or prestressed concrete cross sections.
4.Determination of the maximum stresses and actual stiffnesses for the defined material
law.

I don’t see how it can calculate internal force.

[sfr]

Just try it (calculate e.g. linear elastic stresses and check the "used internal forces in the report)

AQB will rotate the local coordinate system from being parallel to the system line to being parallel to the neutral axis of the beam

Then in general your sectional force are parallel/perpendicular to your section.
In your cgl model the sections are inclined.