Hello,
I would like to present the purpose and methodology of the simulations I’m creating in SOFiSTiK so that I may perhaps learn from feedback from anyone who might be interested.
I am aiming to investigate the effect of the human-structure interaction between pedestrians and a relatively light bridge type of fiber-reinforced polymers, particularly their damping effect on vibrations of the bridge. Humans are known to have this damping effect because of the material they consist of, as opposed to for instance a bag of sand with the same mass, which would have no damping effect. As such, humans can be characterized by a spring constant and damping coefficient of which values can be found in literature.
In my model, I add a custom number of pedestrians modeled as single-degree-of-freedom systems on top of the bridge (i.e. a nodal mass connected to the bridge by a spring-damper). A structure like this also has its own structural damping regardless of the pedestrians, which I implement in the SOFiSTiK model as Rayleigh damping by calculating the alpha and beta coefficients from the natural frequencies and damping ratio of the bridge, which are all known values. I do that with the following records in the DYNA program:
GRP NO #grp_lf,#grp_uf,#grp_edge,#grp_sfh,#grp_sfv,#grp_web VAL FULL RADA #alpha RADB #beta
GRP NO #grp_ped,#grp_ped2,#grp_ped3,#grp_pedspring,#grp_ped2spring,#grp_ped3spring,#grp_pednodes,#grp_ped2nodes,#grp_ped3nodes VAL FULL RADA 0 RADB 0
Important here is that the calculated alpha and beta values are only applied to groups that contain parts of the bridge itself, and not the pedestrians. For all groups that contain parts of the pedestrians, I apply an alpha and beta value of 0.
Next, I apply an impulse force to the middle of the bridge and let it vibrate freely. The acceleration data as a function of time can then be extracted, and with a Matlab script I determine the damping ratio which is present in it. My expectation is that if I add no pedestrians on the bridge, the observed damping ratio should be approximately equal to the one I used as input (to calculate the Rayleigh coefficients), and the more pedestrians I add, the higher the damping ratio will rise above the damping ratio of the bridge itself.
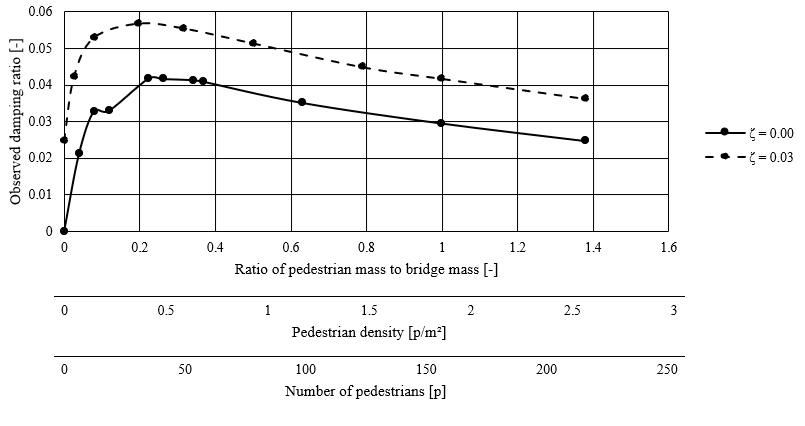
I’ve already done this for a damping ratio of the bridge itself of 0 and of 0.03, and the resulting observed damping ratios are shown in the plot below. It makes sense that it increases at first, but I don’t understand why the observed damping ratio would decrease beyond a certain point. The damping coefficient of the pedestrians themselves (of their SDOF system) corresponds to a damping ratio of 0.3, so I was actually expecting the observed damping ratio of the entire bridge to evolve towards something around 30% as well as more pedestrians are added.
If anyone has thoughts or feedback about my approach, I’d be happy to hear it! My file is also added below:
Puurs v14.dat (71.1 KB)
Kind regards