[Bug Report] Nonlinear Temperature Issue

[netsonic_Sofistik]

Teddy dat is attahced:
1.dat (1.2 KB)

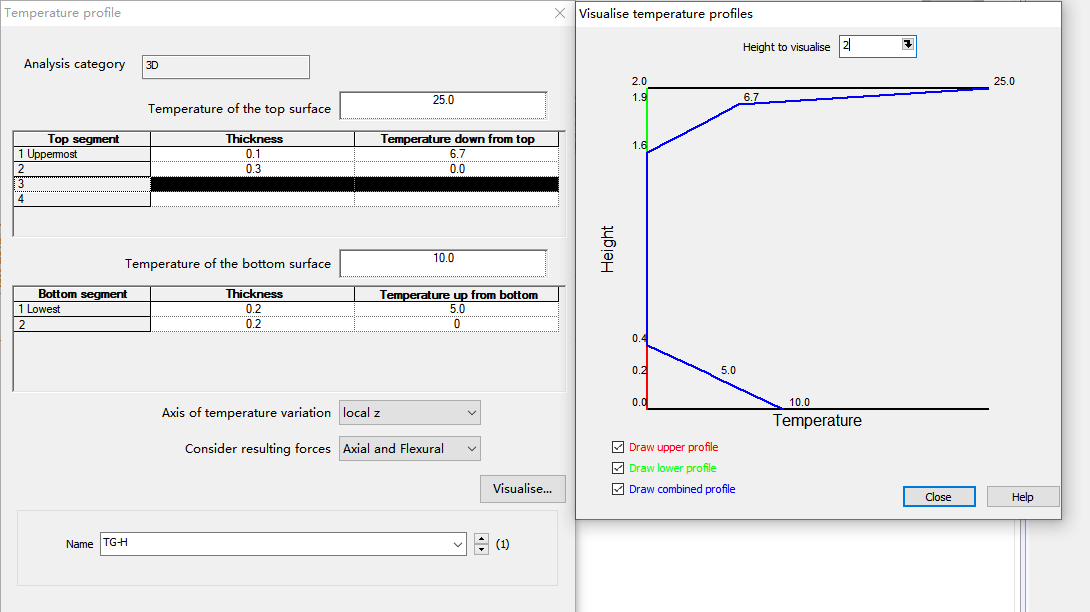
A beam that is fixed at both ends and has two different Nonlinear Temperature profiles (NLTP) on it.
The positive NLTP is as below:
LET#T_H 10 0
LET#Z_H 0 0.5[m]

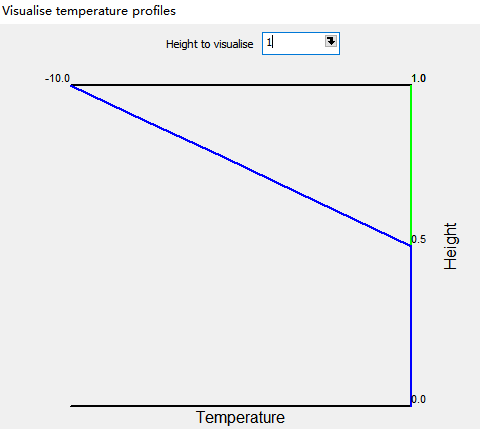
The negative NLTP is as below:
LET#T_C -10 0
LET#Z_C 0 0.5[m]
The negative NLTP has the temperature value that opposite to that of positive NLTP.

I did the analysis by Sofistik 2022-2 and Lusas 19.
The beam has a rectangular cross section. If the height, H <= 1m, the result from Sofistik is correct, the axial force and moment due to negative NLTP are opposite to those due to positive NLTP.
The results from Sofistik are the same as those from Lusas.
The moment in positive NLTP, H=1m
Sofistik = 287.5, the unit is kN*m

Lusas = 287.5, show positve moment in negative value, the unit is N*m

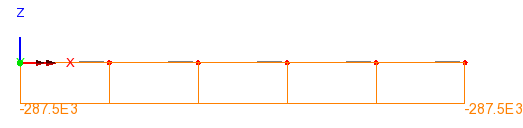
The moment in negative NLTP, H=1m
Sofistik = -287.5

Lusas = -287.5, show negative moment in positive value, the unit is N*m

If the height, H > 1m, the result from Sofistik is WEIRD to me, the axial force and moment due to negative NLTP are much larger than those due to positive NLTP.

The moment in positive NLTP, H=1.1m
Sofistik = 330.6, the unit is kN*m

Lusas = 330.6, show positve moment in negative value, the unit is N*m

The moment in negative NLTP, H=1.1m,
Sofistik = -795.6

Lusas = -330.6

Conclusion:
If H>1m, the results from Sofistik under negative nonlinear temperature profile are questionable.

[netsonic_Sofistik]

I may find the culprit of the above issue.

As for H<=1m, if the negative temperature profile is as follows:
T=-10 Z=0 (Z measured from top of the section)
T=0 Z=0.5m
T=0 Z=1m

you can omit the last point, like this

LET#T_H	-10	0
LET#Z_H	0	0.5[m]

BUT, As for H>1m, if the negative temperature profile is as follows:
T=-10 Z=0 (Z measured from top of the section)
T=0 Z=0.5[m
T=0 Z=1.1m

you CAN NOT omit the last point, like this
this profile will give you WRONG answer.

LET#T_H-	10	0
LET#Z_H	0	0.5[m]

You have to define the profile using all the points, this profile will give you CORRECT answer.

LET#T_H	-10	0	0
LET#Z_H	0	0.5[m]	1.1[m]

@Sofistik
For beam with variable height, define nonlinear temperature profile using all the point espeially the last point at bottom of the beam require user to know the height of the beam. But in most cases, the height of the beam need interpolation by using Aqua INTE. So user do not know in advance the height of those beam that need interpolation.

I suggest Sofistik to learn the Lusas’s way to definea profile:
define from top of the beam and bottom of the beam, then combine them together